I love cryptography. It’s an abstract science, where I can define a problem, come up with a solution and prove it (eventually). I also like applying cryptography as it involves real world (users, limitations of computers, …), which messes everything up and turns pure mathematics into a fun game.

This problem of how to apply cryptography and use it in real systems and products is the main reason, why we hear so much about computer security these days. Cryptographic mechanisms always define some assumptions that are either completely ignored or not so easy to get in the real world (a few historic examples related to randomnes: Netscape, MS Windows, RFID or Java).

We have just launched a cloud PKI service for Amazon AWS – professional PKI system with secure hardware, up and running in under 20 minutes. Not bad for a bunch of guys with a dream to build cloud encryption hardware. Give us thumbs up!

This time, however, I pondered a problem defined by the constraints of an available hardware platform. The hardware platform and other constraints only allowed the clock used as a source of message “freshness” to increment every 30 minutes or so. It would be a long time for a user to wait 30 minutes for each new login or a payment instruction. Users needed to re-login securely much more often so the problem was: how can we make sure that each re-login is secure and can’t be replayed.

To make the problem harder, the new design was a retrofit into an existing system and as such the only added available information on the server-side was an incremental transaction counter (TC). The problem with the TC was that it could get easily de-synchronised and the new protocol had to be able to deal with that.

Direct use of time-based authentication (TOTP) mechanisms (e.g., OATH TOTP)  was out of the question as attackers could re-use the same code or password for up to half an hour. The question was, how to combine the clock with the TC counter while preserving the strength of new logins.

The simplest solution would be to combine a dynamic TOTP code (changing every 30 minutes) with a TC. The final security would then depend on any dictionary attack to raise an alarm / temporarily block the account. Let’s say we are can use 8 digits – simply as any more would be too inconvenient. We end up with 5 digit TOTP code (number changing every 30 minutes) and 3 digits derived from the TC (best is a hash value of TC so that attackers can’t simply increment an eavesdropped value).

This solution is weak against active attackers who can eavesdrop valid codes as they only have to guess 3 digits changing within 30 minute windows.

We could do better due to the nature of authentication. Some authentication methods – and TOTP is one of them – are based on a mechanism where the server repeats the same computation the user did and compares the results. It means that we don’t need to send over the result of the computation but use it has a “master key” or “mask” to securely send something else. You can think about it as a covert channel or a session encryption.

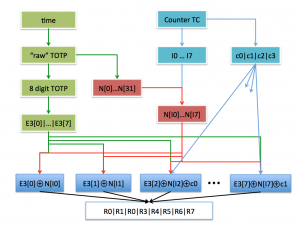The server can re-compute the TOTP value. We can assume it is  a random value as it is a result of a cryptographic hash function or encryption. Also, while we only use 8 digits, the TOTP computation in fact produces 38 digits (128 bits) that the server can also compute.  The hard bit is to find a good way to use the TC counter to boost intra-window entropy as it’s the only information that the server keeps in its database.

I thought we could use the TC to select 8 of the 38 digits in a way that would look random and this is the algorithm I came up with the following:

Note: it is perfectly possible to replace step 6 below with a mechanism based on a hash function. I am open to questions and reviews.

1. Compute E1 the “raw” TOTP – it is a 128 bit number.
2. Compute a cryptographic hash of E1, e.g., E2 = SHA-2(E1).
3. Extract 8 digits from E1 – you can simply compute E3 = E1 mod 10^8 (alternatively finish the OATH TOTP computation). E3 has 8 digits E3[0], E3[1], … E3[7].
4. We will use the counter TC that can be between 0 and 9999. We split the value of TC into orders and units c0, c1, c2 and c3, such that c0*1000+c1*100+c2*10+c3 = TC.
5. We split the E2 value (step 2) into 32 digits – each digit is between 0 and 15. Let’s call them n[i], where i can be 0, 1, 2, … 31.
6. The next step is to find “random” indices. You can either assume the server will try several values of the counter until it gets a match OR we can encode the counter into the code sent over to the server. Here’s a scheme for the latter based on multiplications modulo prime number:
   1. Compute first two indices: I0 = TC*89 mod 97, I1 = TC*83 mod 97.
   2. We now derive a starting_index = (ind0*10+ind1) mod 32.
   3. The remaining 6 indices are Ix = (starting_index * PMx) mod 31. PMx are 29, 23, 19, 17, 13, and 11 respectively (x = 2 … 7).
7. We will now mask the TC value into the final code. This is done one digit at a time: R0 = (I0 + E3[0]) mod 10, R1 = (I1 + E3[1]) mod 10, R2 = (n[I2] + E3[2] + c0) mod 10, R3 = (n[I3] + E3[3] + c1) mod 10, R4 = (n[I4] + E3[4] + c2) mod 10, R5 = (n[I5] + E3[5] + c3) mod 10, R6 = (n[I6] + E3[6] + c0) mod 10, R7 = (n[I7] + E3[7] + c1) mod 10.
8. The authentication code is then of 8 digits R0|R1|R2|R3|R4|R5|R6|R7.

Verification of the code on the server side repeats steps 1-6. The verification of the code in step 7 contains several sources of entropy for security checks.

• the TC counter is included in the result twice – so not only the value should be “in the future” but it should be in two copies.
• Values derived from I0 and I1 can be extracted directly after the OTP value is removed so that the server can quickly detect de-synchronization and adjust its TC value.

I tried to introduce as much randomness into the scheme as possible. The hash of the “raw TOTP” – E3 – is used as a source of random numbers and values I0 … I7 derived from the counter should provide a unique set of random numbers that shouldn’t leak the actual counter value.